Eular法とRunge-Kutta法をPythonで実装する
備忘のために。数値解析関連の話はほとんど学んだことがないため、何か間違いがあるかも。
Eular法
以下、例に出そうとしている微分方程式が運動方程式なので、文字の使い方を力学っぽくしている(位置、速度、時間を $x, v, t$ みたいな気持ちで書いている)。
導出(1階)
まず次の常微分方程式がある。
\[ \frac{dx}{dt} = f(t, x) \]
上の式を以下のように近似する。$h$を十分小さくすれば、微分の定義より上の式に近づく。
\[ \begin{aligned} \frac{x(t + h) - x(t)}{h} \simeq f(t, x) \\ \Rightarrow x(t + h) \simeq x(t) + f(t, x)h \end{aligned} \]
これが、$x(t)$の更新式となっている。つまり、ある時刻$t_0$における値$x_0 = x(t_0)$を決めておけば、
\[ \begin{aligned} & t_k := t_{k-1} + h\\ \end{aligned} \]
とおいて、
\[ \begin{aligned} & x(t_1) := x(t_0) + f(t_0, x_0)h \\ & x(t_2) := x(t_1) + f(t_1, x_1)h \\ & x(t_3) := x(t_2) + f(t_2, x_2)h \\ & … \end{aligned} \]
これは無限に続けられるので、プログラムではどこかのタイミングで停止させる。
ということで、Eular法で必要な要素は以下の5つ。
- 解くべき微分方程式
- 初期時刻 $t_0$ と初期値 $x(t_0)$
- 終了時刻 $t_e$
- 刻み幅 $h$
コード
手でも解ける次の微分方程式を、あえてEular法で解く。
\[ \frac{dx}{dt} = -x,\ x(0) = 1; \]
from matplotlib import pyplot as plt
import numpy as np
def eular(f, t0, x0, te, h):
ts = np.arange(t0, te, h);
xs = []
x = x0
for t in ts:
xs.append(x)
x = x + f(t, x)*h
return (ts, np.array(xs))
f = lambda t, x: -x
ts, xs = eular(f, 0, 1, 10, 0.1)
fig, ax = plt.subplots()
ax.plot(ts, xs)
plt.show()
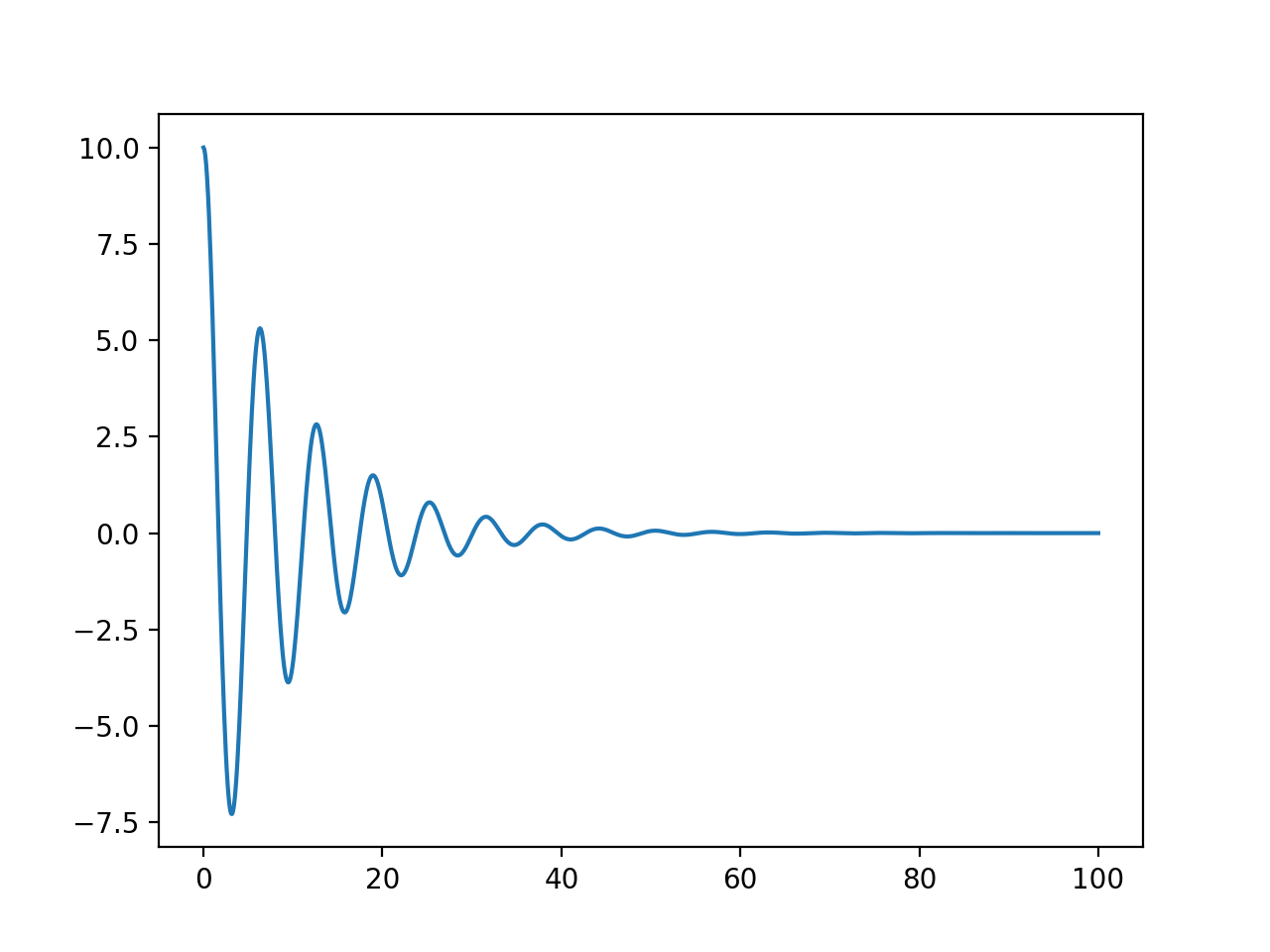
グラフは以下のようになる。
導出(2階)
まず次の常微分方程式がある。
\[ \begin{aligned} &\frac{dx}{dt} = v \\ &\frac{d^2x}{dt^2} = f(t, v, x) \end{aligned} \]
これは次のように書き換えられる。つまり、$v$と$x$の連立方程式と捉えられる。
\[ \begin{aligned} &\frac{dx}{dt} = v \\ &\frac{dv}{dt} = f(t, v, x) \end{aligned} \]
前と同じ議論によって、以下の形にできる。
\[ \begin{aligned} &x(t + h) \simeq x(t) + vh \\ &v(t + h) \simeq v(t) + f(t, v, x)h \end{aligned} \]
これが更新式。
2階の常微分方程式は、初期条件が2つ必要なことに注意。以下では、$t_0$における位置、速度をそれぞれ $x_0, v_0$ とおいている。
コード
減衰振動の方程式を解いてみる。
\[ \begin{aligned} &\frac{dx}{dt} = v \\ &\frac{dv}{dt} = -\omega^2x - kv\\ &v(0) = 0\\ &x(0) = 10 \end{aligned} \]
今回は、適当に $\omega^2 = 1, k = 0.2$ とする。
from matplotlib import pyplot as plt
import numpy as np
def eular(f, t0, x0, v0, te, h):
ts = np.arange(t0, te, h);
xs = []
vs = []
x = x0
v = v0
for t in ts:
xs.append(x)
vs.append(v)
[v, x] = [v + f(t, v, x)*h, x + v*h]
return (ts, np.array(xs))
f = lambda t, v, x: -x - 0.2 * v
ts, xs = eular(f, 0, 10, 0, 100, 0.1)
fig, ax = plt.subplots()
ax.plot(ts, xs)
plt.show()
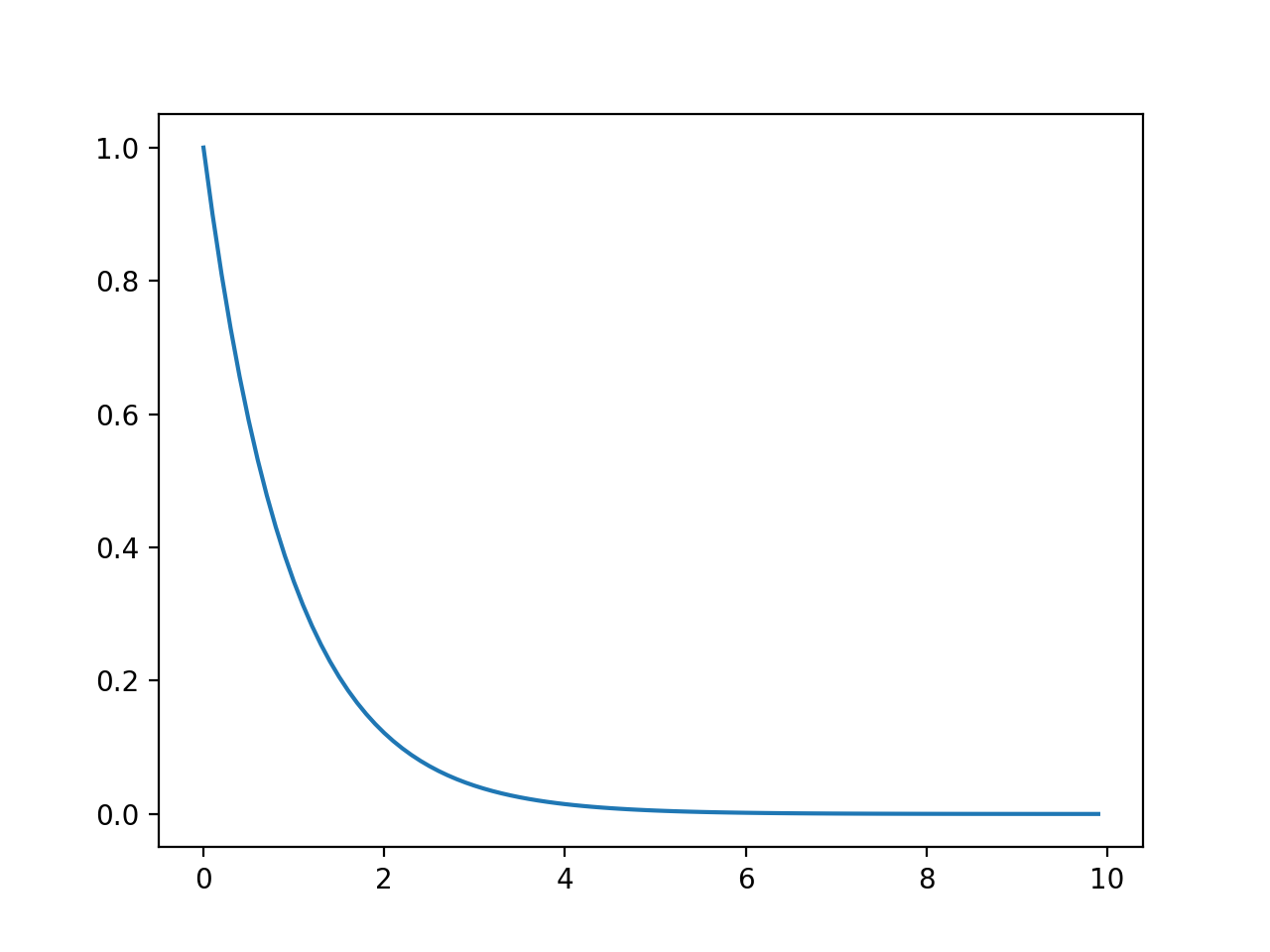
グラフは以下のようになる。
注意
[v, x] = [v + f(t, v, x)*h, x + v*h]
と
v = v + f(t, v, x)*h
x = x + v*h
は意味が違うことに注意。
前者は
\[ \begin{aligned} &v_k := v_{k-1} + f(t_{k-1}, v_{k-1}, x_{k-1})h\\ &x_k := x_{k-1} + v_{k-1}h \end{aligned} \]
という意味だが、後者は、
\[ \begin{aligned} &v_k := v_{k-1} + f(t_{k-1}, v_{k-1}, x_{k-1})h\\ &x_k := x_{k-1} + v_{k}h \end{aligned} \]
という意味になってしまう。つまり、$x_k$を計算するときに$v_k$を使ってしまうことになる。
このような違いが出てしまうのは、コードの実行には順序があることと、変数の再代入ができることが原因。
誤差
Eular法はあまり精度が良くない。例えば、単振動の運動方程式を解くと、誤差が目立つ。
\[ \begin{aligned} &\frac{dx}{dt} = v \\ &\frac{dv}{dt} = -\omega^2x\\ &v(0) = 0\\ &x(0) = 10 \end{aligned} \]
$\omega^2 = 1$ とする。
# eular法のコードは略
f = lambda t, v, x: -x
ts, xs = eular(f, 0, 10, 0, 100, 0.1)
fig, ax = plt.subplots()
ax.plot(ts, xs)
plt.show()
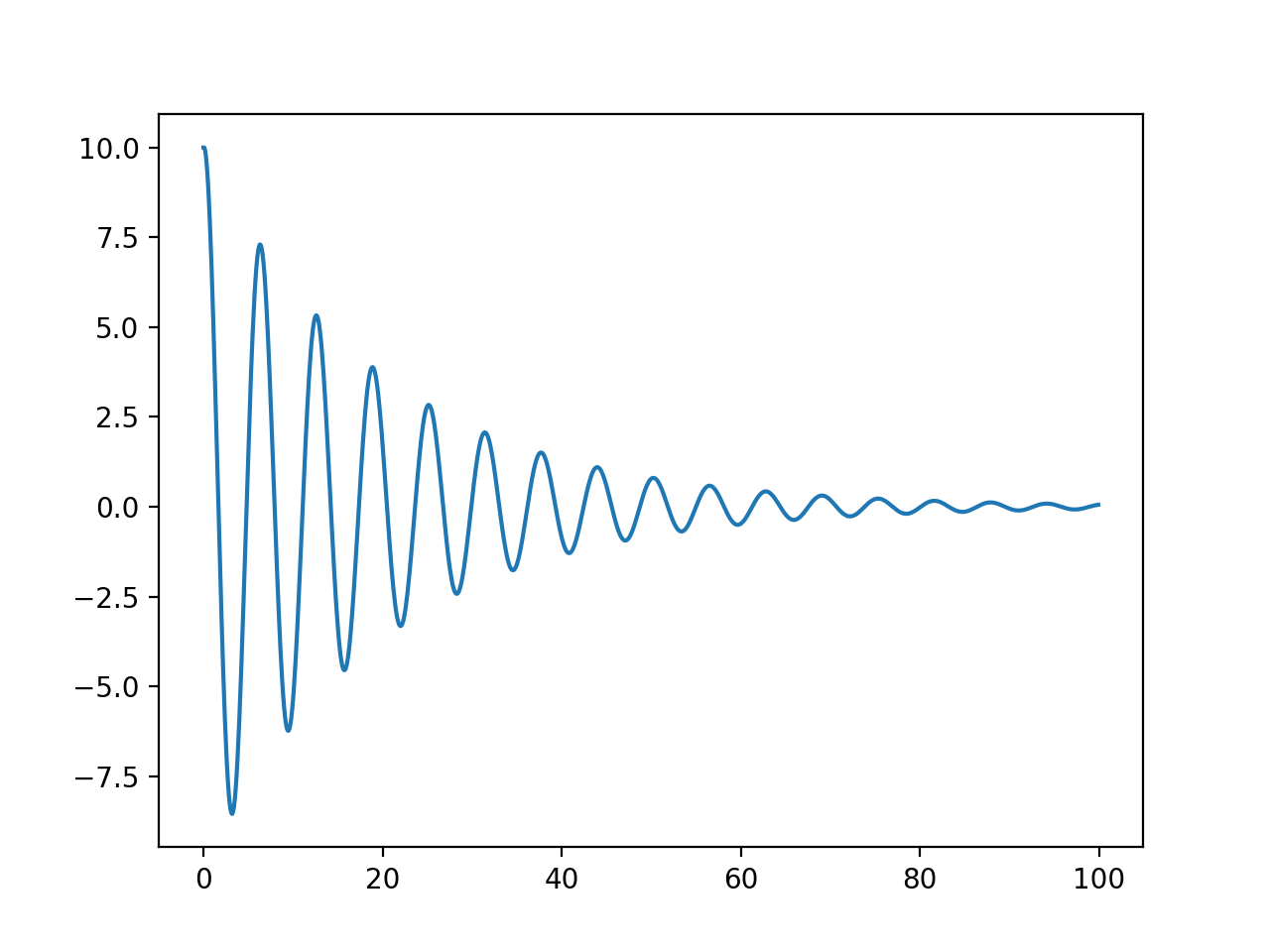
単振動なのに、振幅がどんどん大きくなっている。
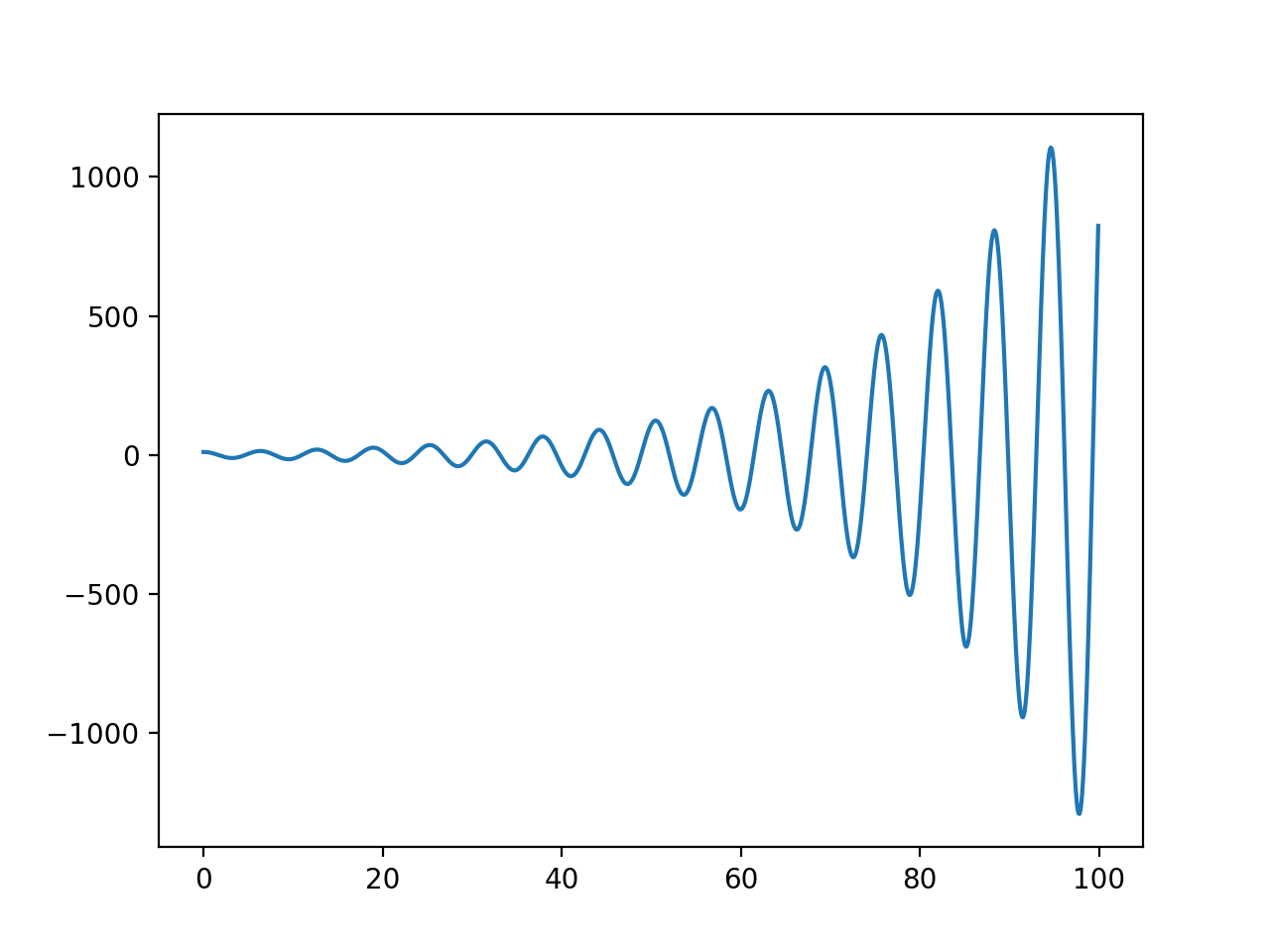
理由は、以下の式
\[ \begin{aligned} x(t + h) &\simeq x(t) + f(t, v, x)h\\ &= x(t) + \dot{x}(t)h \end{aligned} \]
が、$x(t+h)$ の $h$ まわりのTaylor展開において、2次以上の項を切り落とした式になっているからである。その切り落としの部分が誤差になっている。更新の度に誤差が積もっていくことが、グラフからもよくわかる。
Eular法より少し良い方法
1階の場合
\[ \frac{dx}{dt} = f(t, x) \]
Eular法ではいわゆる「一次近似」を利用していた。それなら二次の項まで使えば、精度が上がりそうである。
\[ x(t+h) \simeq x(t) + \dot{x}(t)h + \frac{1}{2}\ddot{x}(t)h^2 \]
$\dot{x}(t) = f(t, x)$ だが、 $\ddot{x}(t)$ の値が分からない。何かの値で代用する必要がある。
そこで(若干飛躍があるかもしれないが)、以下の式が上の等式と一致するように係数$a, b$を決める。
\[ x(t+h) \simeq x(t) + (a\dot{x}(t) + b\dot{x}(t + h))h \]
これは、一次近似により、
\[ \dot{x}(t + h) \simeq \dot{x}(t) + \ddot{x}(t)h \]
だから、
\[ x(t+h) \simeq x(t) + (a + b) \dot{x}(t) + b\dot{x}(t + h)h^2 \]
係数比較により、$a = b = \frac{1}{2}$ とわかる。
これより、
\[ x(t+h) \simeq x(t) + \frac{\dot{x}(t) + \dot{x}(t + h)}{2}h \]
を元にして更新を行えば、より良い精度が得られそうである。ところが、$\dot{x}(t+h)$ の値もそのままでは計算できない。なぜなら、$\dot{x}(t) = f(t, x)$ は実際には $\dot{x}(t) = f(t, x(t))$ と書くべきで、これを考慮すると$\dot{x}(t+h)$は
\[ \dot{x}(t + h) = f(t + h, x(t + h)) \]
と表せて、結局 $x(t + h)$の値が分からないからである。ここはもう仕方ないので、一次近似により、
\[ \begin{aligned} \dot{x}(t + h) &\simeq f(t + h, x(t) + \dot{x}(t)h)\\ &= f(t + h, x(t) + f(t, x)h) \end{aligned} \]
とする。
以上により、次の手順で$x(t)$から$x(t + h)$を算出すればよい。
\[ \begin{aligned} &k_1 := f(t, x(t))\\ &k_2 := f(t + h, x(t) + k_1h)\\ &x(t + h) := x(t) + \frac{k_1 + k_2}{2}h \end{aligned} \]
2階の場合
\[ \begin{aligned} &\frac{dx}{dt} = v(t)\\ &\frac{dv}{dt} = f(t, v(t), x(t)) \end{aligned} \]
上と同じ議論を行うと、次の式が得られる。
\[ \begin{aligned} &v(t + h) \simeq v(t) + \frac{\dot{v}(t) + \dot{v}(t + h)}{2}h\\ &x(t + h) \simeq x(t) + \frac{\dot{x}(t) + \dot{x}(t + h)}{2}h \end{aligned} \]
$v(t + h)$と$x(t + h)$はそのままでは計算できないので、次のように近似する。
\[ \begin{aligned} \dot{v}(t + h) &= f(t + h, v(t + h), x(t + h))\\ &\simeq f(t + h, v(t) + f(t,v,x)h, x(t) + v(t)h)\\ \dot{x}(t + h) &= v(t + h)\\ &\simeq v(t) + f(t,v,x)h \end{aligned} \]
これにより、次の手順が得られる。
\[ \begin{aligned} k_1 &:= f(t, v(t), x(t))\\ l_1 &:= v(t)\\ k_2 &:= f(t + h, v(t) + k_1h, x(t) + l_1h)\\ l_2 &:= v(t) + k_1h\\ v(t + h) &:= v(t) + \frac{k_1 + k_2}{2}h\\ x(t + h) &:= x(t) + \frac{l_1 + l_2}{2}h \end{aligned} \]
コード
さて、この手順を導出するために、何回か近似を行っている。本当にEular法よりも精度が良くなっているのだろうか。試しにコードを組んでみる。
# eular法のコードは略
def eular_improved(f, t0, x0, v0, te, h):
ts = np.arange(t0, te, h);
xs = []
vs = []
x = x0
v = v0
for t in ts:
xs.append(x)
vs.append(v)
k1 = f(t, v, x)
l1 = v
k2 = f(t, v + k1*h, x + l1*h)
l2 = v + k1*h
v = v + (k1 + k2)/2*h
x = x + (l1 + l2)/2*h
return (ts, np.array(xs))
fig, ax = plt.subplots()
ax.set_ylim(-50, 50)
f = lambda t, v, x: -x
ts, xs = eular(f, 0, 10, 0, 100, 0.1)
ax.plot(ts, xs)
ts, xs = eular_improved(f, 0, 10, 0, 100, 0.1)
ax.plot(ts, xs)
plt.show()
次のようなグラフが得られる(青:Eular法、橙:今回の方法)。Eular法に比べて、かなり精度が良くなっている。
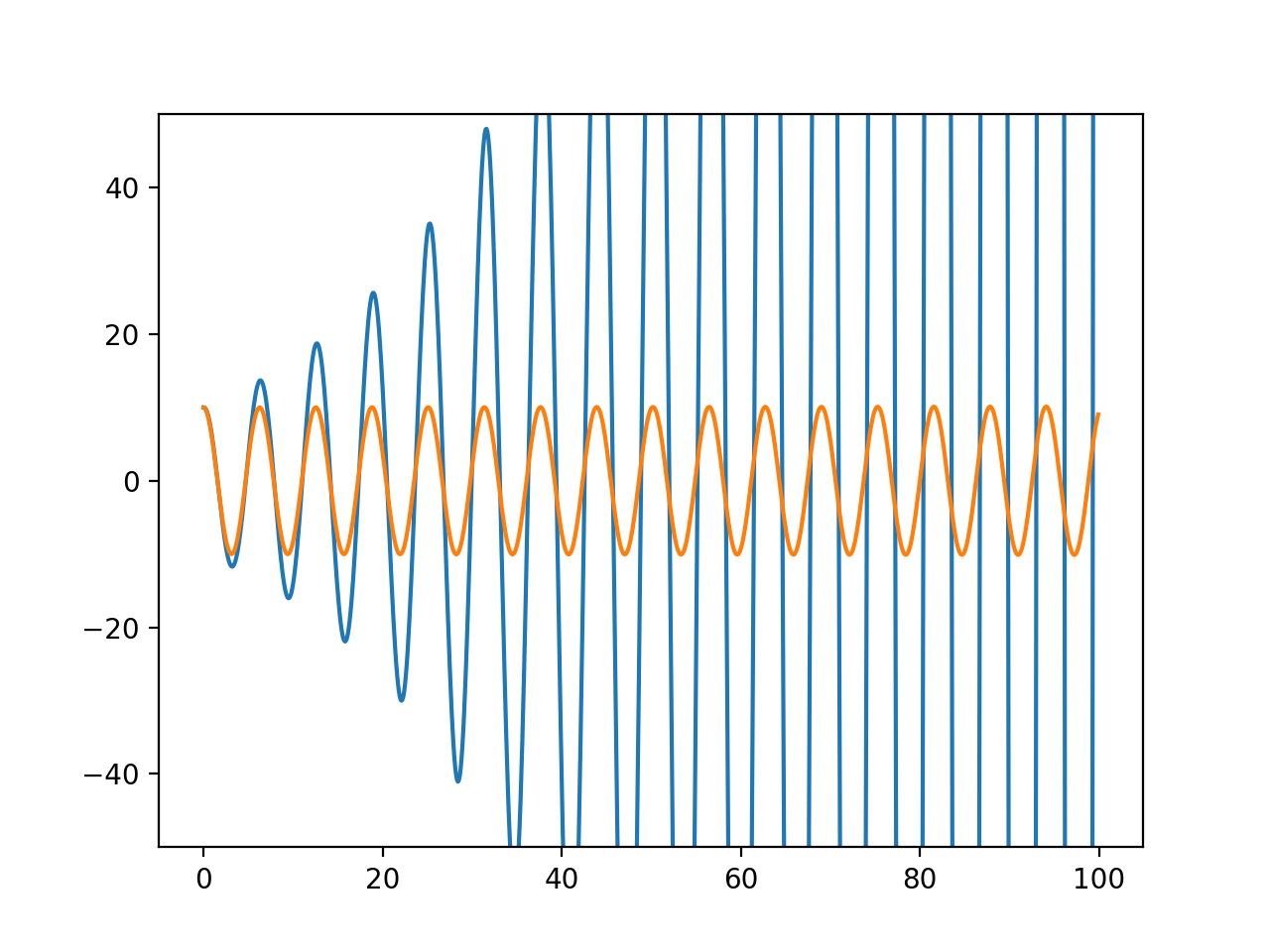
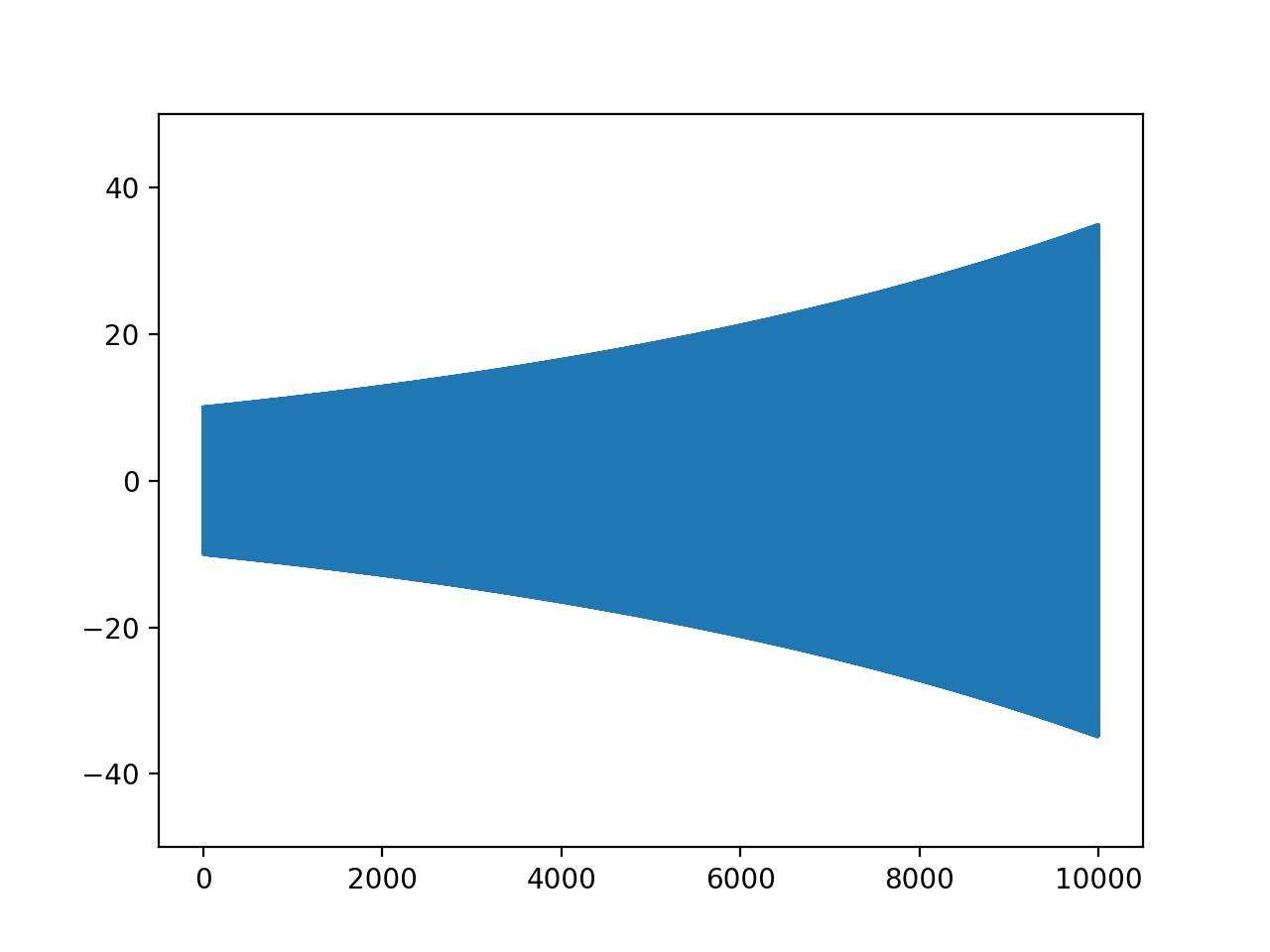
これくらい時間を増やすと、誤差が目に見えてくる。
ts, xs = eular_improved(f, 0, 10, 0, 10000, 0.1)
Runge-Kutta法
もっと良い精度で微分方程式を解くのが、Runge-Kutta法である。
1階の場合。
\[ \frac{dx}{dt} = f(t, x) \]
Runge-Kutta法では、以下のような更新式に従う。導出については詳しく追えていないので、結果だけ示す。恐らく前節と同じような議論を行えば良いのだと思う。Runge-Kutta法にはいくつかの種類がある、以下の形は古典的Runge-Kutta法と呼ばれるもの。
\[ \begin{aligned} x(t + h) &:= x(t) + \frac{k_1 + 2k_2 + 2k_3 + k_4}{6}h\\ k_1 &:= f(t, x(t))\\ k_2 &:= f\left(t + \frac{h}{2}, x(t) + \frac{h}{2}k_1\right)\\ k_3 &:= f\left(t + \frac{h}{2}, x(t) + \frac{h}{2}k_2\right)\\ k_4 &:= f\left(t + h , x(t) + \frac{h}{2}k_3\right) \end{aligned} \]
2階の場合。
\[ \begin{aligned} &\frac{dx}{dt} = v(t)\\ &\frac{dv}{dt} = f(t, v(t), x(t)) \end{aligned} \]
Runge-Kutta法による更新式は以下のようになる。こちらは前節の類推で作っただけなので、合ってるか少し不安。
\[ \begin{aligned} v(t + h) &:= v(t) + \frac{k_1 + 2k_2 + 2k_3 + k_4}{6}h\\ k_1 &:= f(t, v(t), x(t))\\ k_2 &:= f\left(t + \frac{h}{2}, v(t) + \frac{h}{2}k_1, x(t) + \frac{h}{2}l_1\right)\\ k_3 &:= f\left(t + \frac{h}{2}, v(t) + \frac{h}{2}k_2, x(t) + \frac{h}{2}l_2\right)\\ k_4 &:= f\left(t + h , v(t) + hk_3 , x(t) + hl_3\right)\\ \\ x(t + h) &:= x(t) + \frac{l_1 + 2l_2 + 2k_3 + l_4}{6}h\\ l_1 &:= v(t)\\ l_2 &:= v(t) + \frac{h}{2}k_1\\ l_3 &:= v(t) + \frac{h}{2}k_2\\ l_4 &:= v(t) + hk_3 \end{aligned} \]
$k_1$と$l_1$を計算すれば、$k_2$と$l_2$が計算できる。それが計算できれば、$k_3$と$l_3$が計算できる。同様に、$k_4$と$l_4$が計算できる。プログラムでは、この順で計算すれば良い。
コード
単振動の方程式を解いてみる。
\[ \begin{aligned} &\frac{dx}{dt} = v \\ &\frac{dv}{dt} = -x\\ &v(0) = 0\\ &x(0) = 10 \end{aligned} \]
def runge_kutta(f, t0, x0, v0, te, h):
ts = np.arange(t0, te, h);
xs = []
vs = []
x = x0
v = v0
for t in ts:
xs.append(x)
vs.append(v)
k1 = f(t, v, x);
l1 = v
k2 = f(t + h/2, v + h/2*k1, x + h/2*l1)
l2 = v + h/2*k1
k3 = f(t + h/2, v + h/2*k2, x + h/2*l2)
l3 = v + h/2*k2
k4 = f(t + h, v + h*k3, x + h*l3)
l4 = v + h*k3
v = v + (k1 + 2*k2 + 2*k3 + k4)/6*h
x = x + (l1 + 2*l2 + 2*l3 + l4)/6*h
return (ts, np.array(xs))
fig, ax = plt.subplots()
f = lambda t, v, x: -x
ts, xs = runge_kutta(f, 0, 10, 0, 100, 0.1)
ax.plot(ts, xs)
plt.show()
ちゃんと正弦波を描いている。
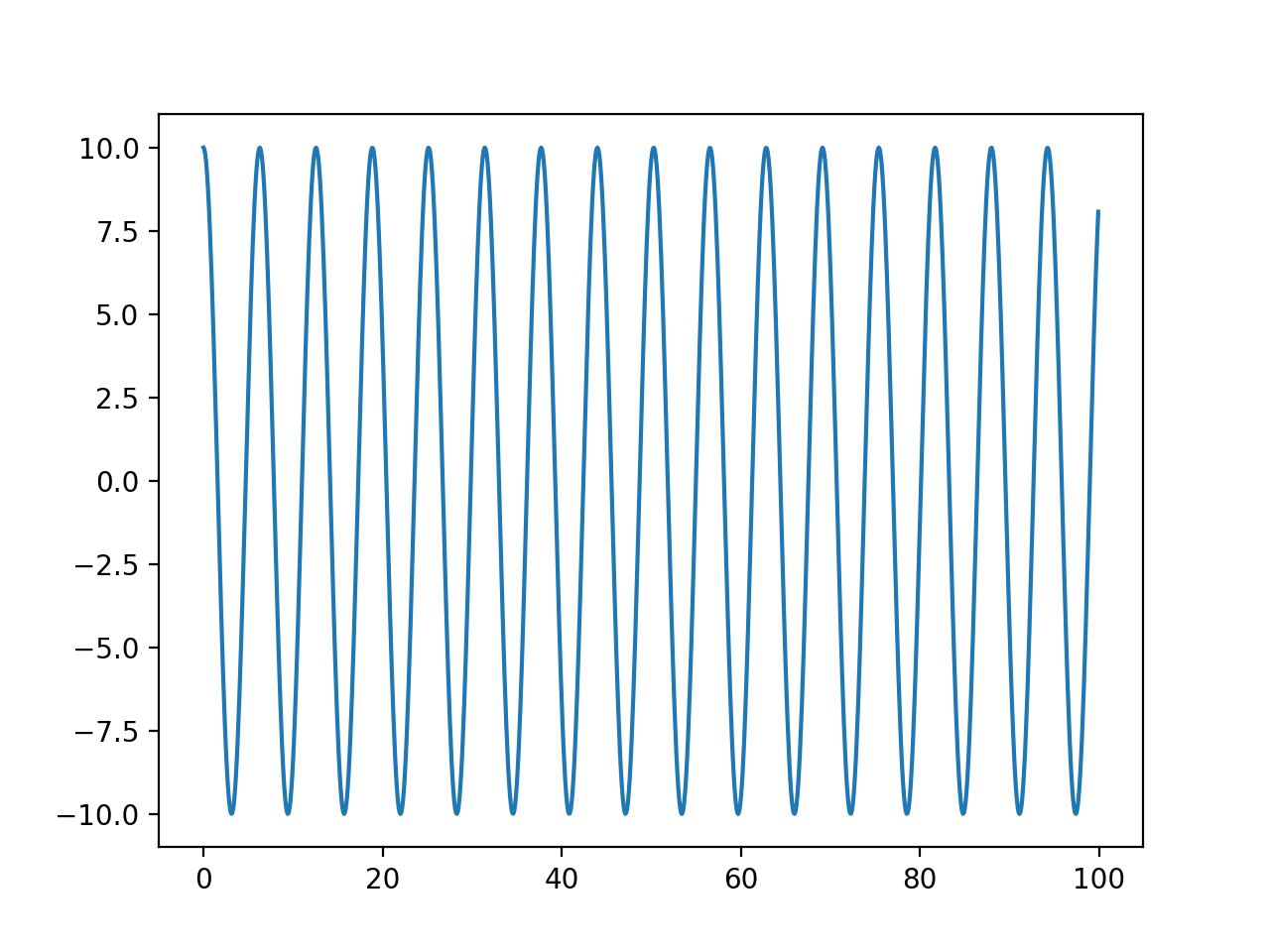
前節の方法と比較してみる。
ax.set_ylim(-50, 50)
ts, xs = eular_improved(f, 0, 10, 0, 10000, 0.1)
ax.plot(ts, xs)
ts, xs = runge_kutta(f, 0, 1, 0, 10000, 0.1)
ax.plot(ts, xs)
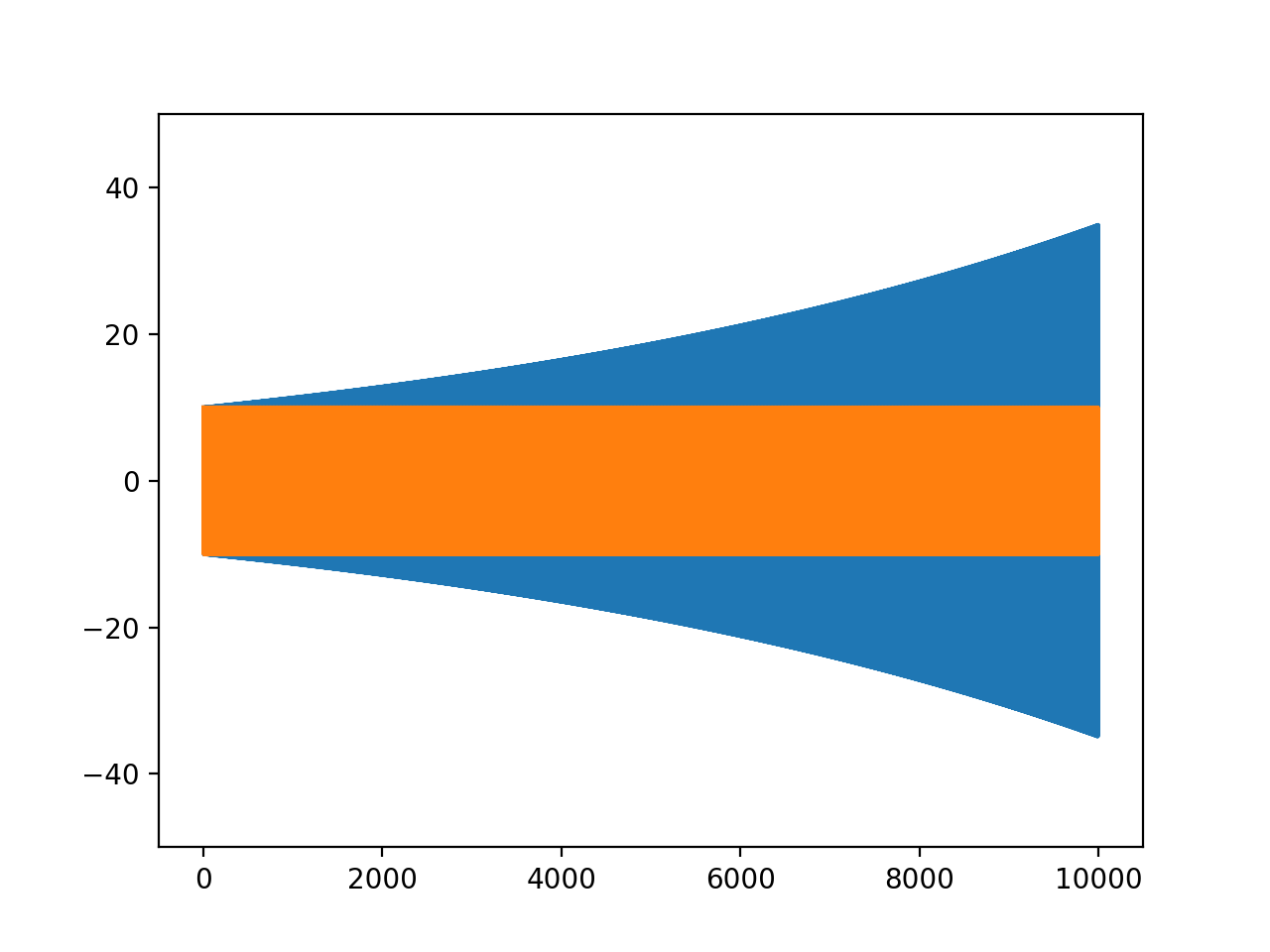
グラフは次のようになる(青:前節の方法、橙: Runge-Kutta法)。Runge-Kutta法の方が精度が良いことが分かる。
ライブラリを使う(SciPy)
以上、頑張って色々書いたが、自分でコードを一から書くとバグを含む可能性があるので、ライブラリを素直に使った方がよい。幸運にも、SciPyに常微分方程式の関数がある。
scipy.integrate.solve_ivpを使う。
以下、リファレンスから抜粋。デフォルトだとRunge-Kutta法になるみたい。
scipy.integrate.solve_ivp(fun, t_span, y0)
これは、次の微分方程式の解を計算してくれる。t_spanはtの範囲のことで、タプル(t0, t_end)のように指定する。刻み幅は適当に決めてくれる。y0はt = t0のときの初期値。
\[ \frac{d\boldsymbol{v}}{dt} = f(t, \boldsymbol{v}) \]
コード
減衰振動の微分方程式をベクトルで表記する。
\[ \begin{aligned} \frac{d}{dt} \left( \begin{matrix} x \\ v \end{matrix} \right) &= \left( \begin{matrix} v \\ -\omega^2x -kv \end{matrix} \right)\\ \left(\begin{matrix} x(0) \\ v(0) \end{matrix}\right) &= \left(\begin{matrix} 10 \\ 0 \end{matrix}\right) \end{aligned} \]
ここでは、$\omega^2 = 1$、$k=0.2$とする。
$x$をv[0]、$v$をv[1]の気持ちで、次のように書く。solver.tで時刻の列、solver.yでそれに対する値の列を取得できる。
import matplotlib.pyplot as plt
import numpy as np
from scipy.integrate import solve_ivp
fig,ax = plt.subplots()
f = lambda t,v: [v[1], -v[0] - 0.2*v[1]]
t_end = 100
solver = solve_ivp(f, (0, t_end), [10, 0])
t = solver.t
v = solver.y
ax.plot(t, v[0])
plt.show()
ただ、このコードだと、グラフがギザギザになっている。
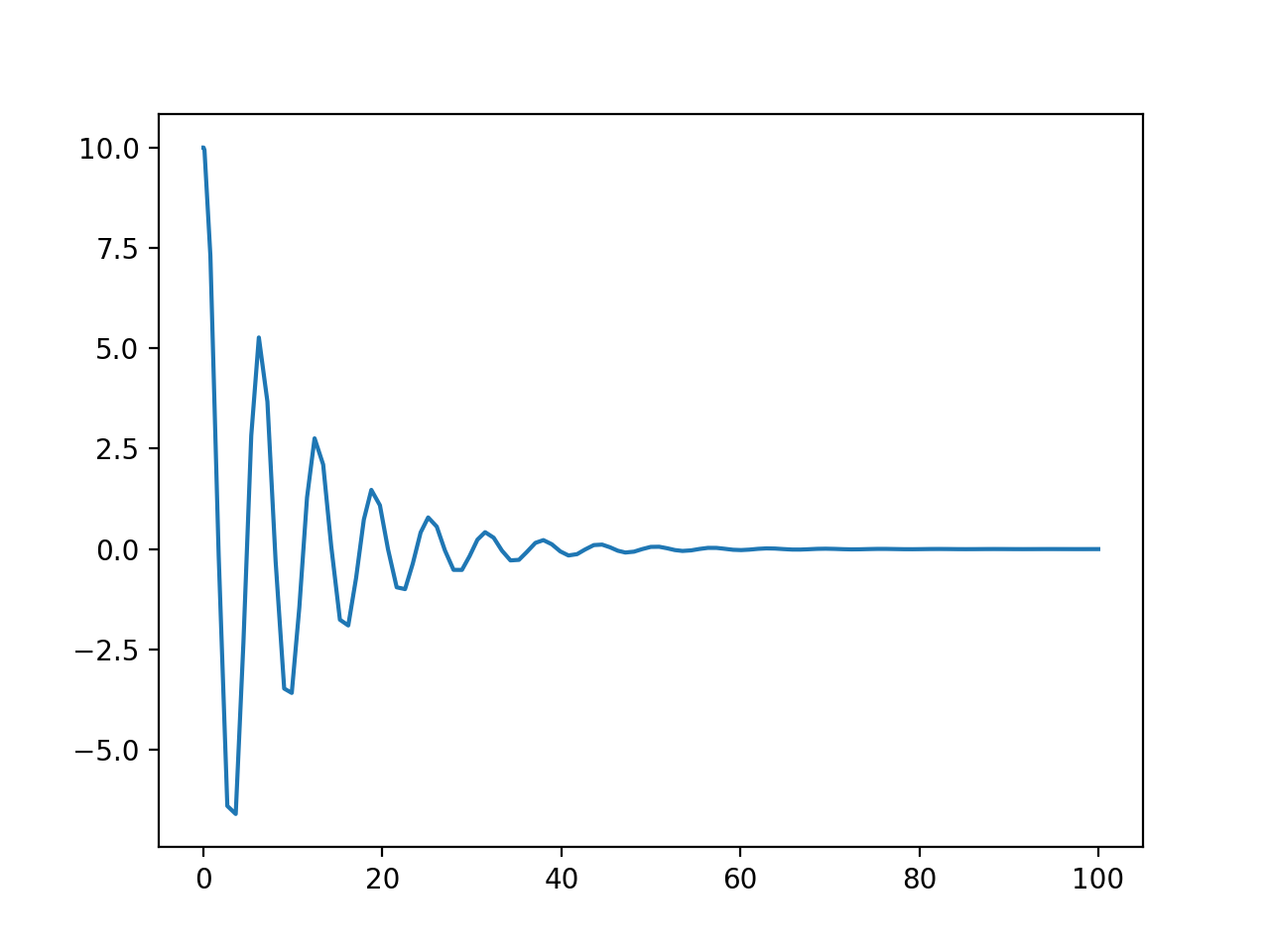
もっと滑らかなものが欲しい場合、次のようにする。solve_ivpの引数にdense_output=Trueを追加し、solver.solで時刻ごとの値を計算する。
import matplotlib.pyplot as plt
import numpy as np
from scipy.integrate import solve_ivp
fig,ax = plt.subplots()
f = lambda t,v: [v[1], -v[0] - 0.2*v[1]]
t_end = 100
solver = solve_ivp(f, (0, t_end), [10, 0], dense_output=True)
t = np.arange(0, t_end, 0.1)
v = solver.sol(t)
ax.plot(t, v[0])
plt.show()