線形回帰メモ 最小二乗法

学校の授業で勉強はしたが、自分で考えてまとめたことはなかったのでここに記しておく。

問題設定(1)

$\bm{y} = (y^{(1)}, y^{(2)}, \ldots, y^{(N)})^T,\ \bm{x}_i = (1, x_1^{(i)}, x_2^{(i)}, \ldots, x_D^{(i)})^T$ とおく。$(\bm{x}_i, y_i),\ i = 1, 2, \ldots, N$ がデータとして与えられている。このとき、入力と出力の間に

$$ \begin{aligned} y &= h_{\bm{w}}(\bm{x})\\ &:= w_0 + w_1x_1 + w_2x_2 + \cdots + w_Dx_D\\ &= \bm{w}^T\bm{x} \end{aligned} $$

が成り立つと仮定し、これに適する$\bm{w}$を見つけたい。「適する」とは具体的に何なのかというと、ここでは予測とデータとの二乗誤差の和

$$ J(\bm{w}) = \frac{1}{2} \sum_{i=1}^{N} (h_{\bm{w}}(\bm{x}_i) - y^{(i)})^2 $$

が最小となる $\bm{w}$ を求める。この $J$ については呼び名がいくつかあるが、ここではコスト関数と呼ぶ。 係数 $1/2$ は微分した時に出てくる $2$ を消し去るための便宜的なものであり、つける必然はない。

コスト関数の最小値を求める(1)

コスト関数の行列表現

まず $J$ を行列だけで表現してみる。

ここで、

$$ X = \begin{pmatrix} \bm{x}_1^T \\ \bm{x}_2^T \\ \vdots \\ \bm{x}_N^T \end{pmatrix} $$

とおくと、

$$ \begin{aligned} J(\bm{w}) &= \frac{1}{2} \left( \begin{pmatrix} \bm{x}_1^T\bm{w}\\ \bm{x}_2^T\bm{w}\\ \vdots\\ \bm{x}_N^T\bm{w}\\ \end{pmatrix} - \bm{y} \right)^T \left( \begin{pmatrix} \bm{x}_1^T\bm{w}\\ \bm{x}_2^T\bm{w}\\ \vdots\\ \bm{x}_N^T\bm{w}\\ \end{pmatrix} - \bm{y} \right)\\ &= \frac{1}{2} \left( X\bm{w} - \bm{y} \right)^T \left( X\bm{w} - \bm{y} \right) \end{aligned} $$

コスト関数の勾配

$J$ の勾配を求めるために、式を展開する。

$$ \begin{aligned} J(\bm{w}) &= \frac{1}{2} \left( \bm{w}^TX^T - \bm{y}^T \right) \left( X\bm{w} - \bm{y} \right)\\ &= \frac{1}{2} \left( \bm{w}^TX^TX\bm{w} - \bm{w}^TX^T\bm{y} -\bm{y}^TX\bm{w} + \bm{y}^T\bm{y} \right) \end{aligned} $$

$J$ の全ての項はスカラーだから、$\bm{w}^TX^T\bm{y} = \bm{y}^TX\bm{w}$が成り立つ。よって、

$$ \begin{aligned} J(\bm{w}) &= \frac{1}{2} \left( \bm{w}^TX^TX\bm{w} - 2\bm{y}^TX\bm{w} + \bm{y}^T\bm{y} \right) \end{aligned} $$

二次形式の微分とベクトルの微分

$$ \begin{aligned} \frac{\partial}{\partial \bm{x}} \bm{x}^TA\bm{x} &= (A + A^T) \bm{x} \\ \frac{\partial}{\partial \bm{x}} \bm{a}^T\bm{x} &= \bm{a} \end{aligned} $$

に注意すると、

$$ \begin{aligned} \frac{\partial J(\bm{w})}{\partial \bm{w}} &= \frac{1}{2} \left( (X^TX + (X^TX)^T) \bm{w} - 2X^T\bm{y} \right)\\ &= \frac{1}{2} \left( 2X^TX \bm{w} - 2X^T\bm{y} \right)\\ &= X^TX \bm{w} - X^T\bm{y} \end{aligned} $$

これで勾配が導出できた。係数 $1/2$ がうまく消えてくれたことに注目。

早速"勾配 = 0"を解いてみる。その解を $\bm{w}_0$とすると、$X^TX$が正則であると仮定して、

$$ \begin{aligned} & \quad \frac{\partial J(\bm{w}_0)}{\partial \bm{w}} = \bm{0} \\ \Leftrightarrow & \quad X^TX \bm{w}_0 = X^T\bm{y} \\ \Leftrightarrow & \quad \bm{w}_0 = \left( X^TX \right)^{-1} X^T \bm{y} \end{aligned} $$

極小値であること

さて、これは本当に極小値なのだろうか。 それを確かめるべく、ヘッセ行列を計算してみる。 もし $\bm{w}$ に対応するヘッセ行列が正定値行列なら、それは極小値である。

一般に、 $\displaystyle \frac{\partial f}{\partial \bm{x}} = \bm{a}$ なら $\displaystyle \frac{\partial f}{\partial \bm{x}^T} = \bm{a}^T$ だから、

$$ \begin{aligned} \frac{\partial J(\bm{w})}{\partial \bm{w}^T} &= \bm{w}^TXX^T - \bm{y}^TX^T \end{aligned} $$

よって、ヘッセ行列は、

$$ \begin{aligned} \frac{\partial J(\bm{w})}{\partial \bm{w}^T\bm{w}} &= X^TX \end{aligned} $$

これはどうやら $\bm{w}$ によらない行列になるようだ。 一般に $\bm{x}^T\bm{x} \ge 0$ となることに注意すると、 任意の $\bm{z} \neq \bm{0}$ について、

$$ \begin{aligned} \bm{z}^T(X^TX)\bm{z} = (X\bm{z})^T(X\bm{z}) \ge 0 \end{aligned} $$

であるから、$X^TX$ は半正定値行列である。 このことから、$J$ が凸関数であることがいえる。 しかしこの時点ではまだ極小かどうかは分からない。 $X\bm{z} = \bm{0}$ となる $\bm{z} \neq \bm{0}$ が存在しなければ、$X^TX$ は正定値行列である。

$X \in \mathbb{R}^{N \times (D + 1)}$ が正方行列でない可能性があることに注意すると、 $\bm{z}$ についての同次方程式 $X\bm{z} = \bm{0}$ が自明な解しか持たないための必要十分条件は $\mathrm{rank}\ X = D + 1$、すなわち列フルランクであることである。 一般に $\mathrm{rank}\ X^TX = \mathrm{rank}\ X$ が成り立つ(この事実は今回初めて知った…)。 よって、$\mathrm{rank}\ X = D + 1$ であることと $X^TX$ が正則であることは同値である。$X^TX$ の正則性は仮定していたから、結局 $X^TX$ が正定値であることが分かった。 すなわち、$J(\bm{w}_0)$ は極小値である。

最小値であること

$J$ のヘッセ行列が $\bm{w}$ によらず $X^TX$、すなわち正定値行列であることに注意すると、$J(\bm{w}_0)$ 極小値であるだけでなく、最小値であることも示せる。見やすさのため、 ここでは勾配を $\nabla J(\bm{w})$ 、ヘッセ行列を $\nabla^2 J(\bm{w})$ と書く。 $\bm{w}$ を $\nabla J(\bm{w}) = \bm{0}$ となる点とする。 そこから$\Delta \bm{w}$ だけずれた $J(\bm{w} + \Delta\bm{w})$ を考える。 テイラーの定理より、ある $\bm{d}$ が存在して、

$$ J(\bm{w}_0 + \Delta\bm{w}) = J(\bm{w}_0) + \nabla J(\bm{w}_0)^T \Delta\bm{w} + \frac{1}{2} \Delta \bm{w}^T \nabla^2 J(\bm{d}) \Delta \bm{w} $$

となる。 仮定より $\nabla J(\bm{w}) = \bm{0}$、正定値性より $\Delta \bm{w}^T \nabla^2 J(\bm{d}) \Delta \bm{w} \gt 0$ だから、結局、

$$ J(\bm{w} + \Delta\bm{w}) \gt J(\bm{w}) $$

となる。よって、$\bm{w}$ から $\Delta \bm{w}$ だけずれたとしても、$J$ の値は $J(\bm{w})$ 以下にならない。 よって、$J$ は $\bm{w}$ で大域的な最小値となる。

Juliaによる実装

さて、$X^TX$ が正則であれば、$J$ の最小値は

$$ \begin{aligned} \bm{w}_0 = \left( X^TX \right)^{-1} X^T \bm{y} \end{aligned} $$

で与えられることが分かった。

これを計算するプログラムを書くのは、線型代数のライブラリを持つ言語なら非常に簡単である。 ここではJuliaでプログラムを書いてみる。

ちなみに、Pythonではnumpy.linalgを使えば逆行列とかの計算ができる。 実装を気にすることなく線形回帰をしたい場合は scikit-learnのLinearRegression を使えば良い。scikit-learnのJulia版にScikitLearn.jlがある(内部でscikit-learnを呼び出している模様)ので、 Juliaでも同じことができる。

関連モジュールをインポートし、型のエイリアスを作っておく。

using Plots
using LinearAlgebra
using Random, Distributions

サンプルデータの作成

ここではデータセットは使わず、データは自前で作る。 ある $\bm{w}$ で作ったデータを元に $\bm{w}_0$ を計算して、これが $\bm{w}$ と近い値なのかどうかを確認する。

まず、適当なデータを作成する関数を作る。 $\bm{w}$ が与えられたとすると、作るデータ $(\bm{x}, y)$ は

$$ y = \bm{w}^T\bm{x} + \varepsilon $$

に従うものとする。ただし、 $\varepsilon$ は平均 $0$、分散 $\sigma^2$ の正規分布とする。 $\bm{x} = (1, x_1, x_2, \ldots, x_D)$ の最初の成分以外は一様分布乱数で作成し、さらに正規分布乱数で $\varepsilon$ を計算すれば $\bm{y}$ を計算できる。

$\bm{w}$ を元に $N$ 点のデータを作成する関数は以下のようになる。 少ないデータで結果を出したい都合上、正規分布の標準偏差を小さく設定している。

function generate_data(w, N)
  D = length(w)
  @assert D > 1

  d = Normal(0, 0.1)
  X = hcat(ones(N), rand(N, D - 1))
  y = X * w + rand(d, N)

  X, y
end

作成したデータを試しにプロットしてみたいので、以下のようにmain関数を作成。

function main()
  Random.seed!(2021)

  X, y = generate_data([1.0, 2.0], 100)
  p1 = scatter(X[:, 2], y)

  display(p1)
end

# main関数を実行
main()

ためしにJuliaのREPLで確かめてみる。コードのファイル名はregression.jlとした。

% julia
julia> include("regression.jl")

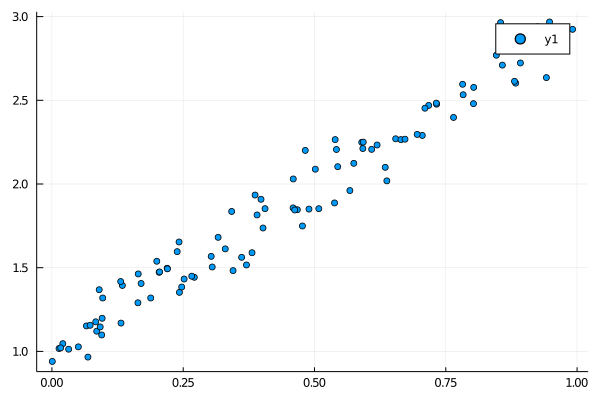
generate_dataの引数を[1.0, 2.0]にしたので、$y = 1 + 2x$ の点がプロットできている。

wの計算

次の計算式をそのままJuliaに書き下せば良い。

$$ \begin{aligned} \bm{w} = \left( X^TX \right)^{-1} X^T \bm{y} \end{aligned} $$

Juliaでは行列の転置を'、逆行列をinvで計算できる。

w =  inv(X' * X) * (X' * y)

…と言いたいところだが、逆行列を計算して左から掛けるよりも、 以下の $\bm{w}$ についての方程式を解く方が、 数値計算の効率が良い。

$$ \begin{aligned} X^TX\bm{w} = X^T \bm{y} \end{aligned} $$

Juliaではこれを\演算子で行える。

w =  (X' * X) \ (X' * y)

試しに $\bm{w} = (-1, 2, 4, 1)$ でデータを生成して、そのうえで w を計算してみる。

function main()
  Random.seed!(2021)

  X, y = generate_data([-1.0, 2.0, 4.0, 1.0], 100)
  p1 = scatter(X[:, 2], y)

  w =  (X' * X) \ (X' * y)
  display(w)
end

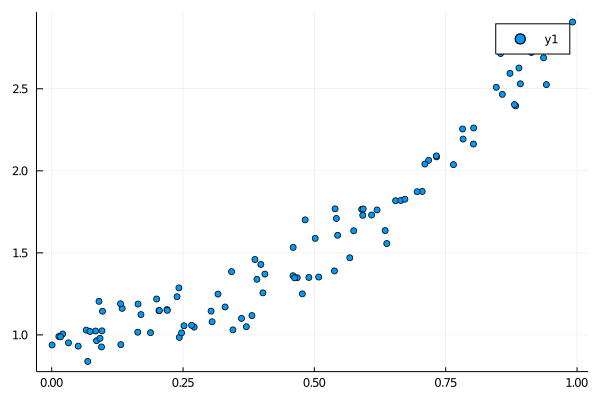
[-1, 2, 4, 1]に近い値になっていることが分かる。

julia> include("regression.jl")
4-element Vector{Float64}:
 -1.06337895821069
  1.9893951252434998
  4.025930296546132
  1.0825520926923566

グラフでプロットして確認してみる。$\bm{w} = (1, 2)$ の場合でwを計算し、 それを係数とした直線を引いてみる。

function main()
  Random.seed!(2021)

  X, y = generate_data([1.0, 2.0], 100)
  p1 = scatter(X[:, 2], y)

  # wの計算
  w =  (X' * X) \ (X' * y)

  # y = w[1] + w[2]*x の描画
  plot_x = range(minimum(X[:, 2]), maximum(X[:, 2]), length=100)
  plot!(p1, plot_x, x -> w[1] + w[2]*x)

  display(p1)
end

julia> include("regression.jl")

データ点に近い直線を引けていることが確認できる。

問題設定(2) - 基底関数を含む場合

$\bm{y} = (y^{(1)}, y^{(2)}, \ldots, y^{(N)})^T,\ \bm{x}_i = (1, x_1^{(i)}, x_2^{(i)}, \ldots, x_{D_0}^{(i)})^T, \bm{\phi}(\bm{x}) = (1, \phi_1(\bm{x}), \phi_2(\bm{x}), \ldots, \phi_D(\bm{x}))$ とおく。$(\bm{x}_i, y_i),\ i = 1, 2, \ldots, N$ がデータとして与えられている。このとき、入力と出力の間に

$$ \begin{aligned} y &= h_{\bm{w}}(\bm{x})\\ &:= w_0 + w_1\phi_1(\bm{x}) + w_2\phi_2(\bm{x}) + \cdots + w_D\phi_D(\bm{x})\\ &= \bm{w}^T\bm{\phi}(\bm{x}) \end{aligned} $$

が成り立つと仮定し、そのコスト関数

$$ \begin{aligned} J(\bm{w}) = \frac{1}{2} \sum_{i=1}^{N} (h_{\bm{w}}(\bm{x}_i) - y^{(i)})^2 \end{aligned} $$

が最小になるように $\bm{w}$ を決定したい。

コスト関数の最小値を求める (2)

流れは「コスト関数最小値を求める(1)」とまったく同じ。

$$ \begin{aligned} \Phi = \begin{pmatrix} \bm{\phi}(\bm{x}_1)^T\\ \bm{\phi}(\bm{x}_2)^T\\ \vdots\\ \bm{\phi}(\bm{x}_N)^T \end{pmatrix} \end{aligned} $$

として、

$$ \begin{aligned} J(\bm{w}) &= \frac{1}{2} \left( \Phi\bm{w} - \bm{y} \right)^T \left( \Phi\bm{w} - \bm{y} \right)\\ &= \frac{1}{2} \left(\bm{w}^T\Phi^T\Phi\bm{w} - 2\bm{y}\Phi\bm{w} + \bm{y}^T\bm{y}\right) \end{aligned} $$

が得られる。続いて勾配を求めると、

$$ \begin{aligned} \frac{\partial J(\bm{w})}{\partial \bm{w}} &= \Phi^T\Phi\bm{w} - \Phi^T\bm{y} \end{aligned} $$

となる。$\Phi^T\Phi$ が正則なら、以下の $\bm{w}$ が存在し、それは $J$ の最小値となる。

$$ \begin{aligned} & \quad \frac{\partial J(\bm{w})}{\partial \bm{w}} = \bm{0}\\ \Leftrightarrow & \quad \bm{w} = \left(\Phi^T\Phi\right)^{-1} \Phi^T\bm{y} \end{aligned} $$

Juliaによる実装 (2)

サンプルデータの作成 (2)

$\Phi$ を計算するために、ベクトル値関数 $\bm{\phi}(\bm{x})$ を引数に持たせる。 $\bm{w}$ の計算にもはや $X$ は必要ないのだが、グラフにデータをプロットする際に必要になるので、 $X$ も返り値に含めている。

function generate_data(N, num_of_var, w, phi)
  dummy = Vector{Float64}(undef, num_of_var)
  D = length(phi(dummy))

  d = Normal(0, 0.1)
  X = hcat(ones(N), rand(N, num_of_var))

  Phi = Matrix{Float64}(undef, N, D + 1)
  for n in 1:N
    Phi[n,1] = 1.0
    Phi[n,2:end] = phi(X[n,2:end])
  end

  y = Phi * w + rand(d, N)
  X, Phi, y
end

試しに関数 $y = 1 + 2x^2$ によるデータをプロットしてみる。

function main()
  Random.seed!(2021)

  X, Phi, y = generate_data(100, 1, [1.0, 2.0], x->[x[1]^2])
  p1 = scatter(X[:, 2], y)

  display(p1)
end

wの計算 (2)

これに対応するwを求める。

function main()
  Random.seed!(2021)

  X, Phi, y = generate_data(100, 1, [1.0, 2.0], x->[x[1]^2])
  p1 = scatter(X[:, 2], y)

  w =  (Phi' * Phi) \ (Phi' * y)
  display(w)

  plot_x = range(minimum(X[:, 2]), maximum(X[:, 2]), length=100)
  plot!(p1, plot_x, x -> w[1] + w[2]*x^2)

  display(p1)
end

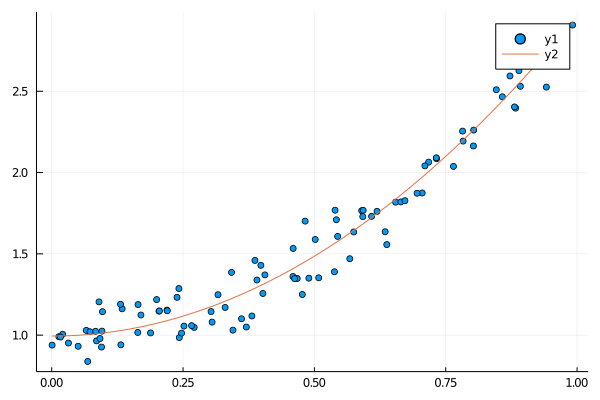
[1, 2]に近い値をとっている。

julia> include("regression.jl")
2-element Vector{Float64}:
 0.9943755135747157
 1.965007135423543

データ点に近い2次関数を描いている。

計算量

以下の $\bm{w}$ を計算するときの時間計算量を考える。

$$ \begin{aligned} X^TX\bm{w} = X^T \bm{y} \end{aligned} $$

Juliaではこれを\演算子で行える。

w =  (X' * X) \ (X' * y)

$X^T\bm{y}$ の計算量は、$D \times N$ 行列と $N \times 1$ 行列の積の計算だから $O(DN)$。

$X^TX$ の計算量は、$D \times N$ 行列と $N \times D$ 行列の積の計算だから $O(ND^2)$。

\ のドキュメントによると、 三角行列の場合は交代代入 or 前進代入、そうでない場合はLU分解で三角行列に変換してから解くようだ。$X^TX$ は一般に三角行列ではないのでLU分解され、計算量は $O(D^3)$ となる。

まとめると、計算量は $O(ND^2 + D^3)$ となる。